量子コンピュータ
イントロダクション量子コンピュータが実現すると、インターネットなどで利用されている重要な暗号システムはすべて崩壊してしまう…、そういったセンセーショナルな内容の記事が、最近になって一般の新聞などで見うけられるようになってきた。 これほど進歩した現在のコンピュータにも苦手な問題というものがあって、その一つに桁数の大きい因数分解が挙げられる。そして、現在の暗号システムというのは因数分解に基づいており、今のコンピュータが現実的な時間内にその解を見つけることができないということで、その安全性を保証している。 ところが量子コンピュータは、従来のものが宇宙誕生からの歴史ほどかかっても解けないような問題を数分か数秒足らずで解いてしまうというのだ。 いったい量子コンピュータとはどういう原理に基づいているのだろう?どんな点で、従来のコンピュータより優れているのだろうか? 今回は、量子コンピュータの特徴や理論、そして、これまでに実証された量子コンピュータのプロトタイプなどを見ながら、量子コンピュータの可能性について探ってみよう。のが、「量子コンピュ-タ」や「DNAコンピュータ」と呼ばれる、まったく新しいタイプのコンピュ-タだ。これらのコンピュータはともに新しい分野で、とても現在のコンピュータに対抗できるようなものではない。しかし、可能性としてはとても大きなものを秘めている。 今回は、そのDNAコンピュータの基本的性質や、最近の研究、そして展望などにスポットライトを当ててみることにしよう。 量子コンピュータの歴史1959 「量子力学的な振る舞い」を計算に利用する 1959年に、Richard FeynmanはCaltech(カルフォルニア工科大学)である公演を行なった。その内容は、原子分子レベルではまだ活かしきれていないスペースが存分にある(“There’s Plenty of room at the bottom”)といったものだった。[1]当時はあちこちで小型化の波が押し寄せ、それに伴って情報の高密度化が進行していたが、それとは一線を引いた内容で議論を行なった。 Feynmanはその公演のなかで、例えば「量子化されたエネルギー準位(quantized energy levels)」や「スピン(quantized spins)」など、量子力学的な振る舞いを利用することを提案した。ただし、このときの話は理論的なものが中心で、具体的な手段については何も触れられていなかった。 実際には、今の量子コンピュータの誕生とこの出来事を直接結びつけるべきではないかもしれない。ただ、量子コンピュータやスピントロニクスが注目されるようになった今に、この公演の内容を振り返ってみると非常に興味深い。
それまで、不確定性原理による理由から、計算過程でエネルギーを消費し、量子的な系の情報が失われてしまうために、どんな量子力学的モデルもコンピュータに利用することはできないと考えられていた。ところが、Paul Benioffは1980年からの一連の論文で、エネルギーを消費せずに計算が行えることを示した。[2]こうして、はじめて量子コンピュータという概念が誕生した。82年には、ノーベル物理学賞を受賞したFeynmannも、この有用性について言及している。 ただし当時は、量子コンピュータはあくまで学術的な興味の範疇にとどまっており、広く関心が集まることはなかった。
90年代に入り、量子コンピュータでどのような問題を解くことができるかが議論されるようになった。しかし、そのなかでも最もインパクトが大きかったのは、94年にベル研のPeter Shorの示した因数分解のアルゴリズムに違いない。[3] 現在の暗号システムは因数分解に基づいており、従来のコンピュータが現実的な時間で因数分解を解くことができないことを、暗号の安全性の根拠としている。ところが、それまで宇宙年ほどの時間(順指数間数的な時間)をかけても解けなかった因数分解を量子コンピュータは数分で解いてしまうことが示されたのだ。 仮に量子コンピュータが実現すると、重要な暗号システムRSAも破られてしまい、社会的な影響は非常に大きい。こうなれば、インターネットもメールも携帯電話もすべて信用できなくなってしまう…。 こうして量子コンピュータは強烈なインパクトとともに、広く注目されるようになった。
こうして、量子コンピュータが理論どうりに実現されれば、現在のコンピュータよりも本質的に高速なコンピュータが得られる理論的状況証拠はすでに示された。ただ問題は、量子コンピュータのハードウェアを技術的につくることが恐ろしく難しいということだった。 90年の後半に入って、世界中のいくつかの研究所で、数キュービット(量子ビット)の量子コンピュータの動作が実証されるようになった。これらのハードウェアというのは現在のコンピュータと比べるとずいぶん風変わりなもので、例えば、低温でイオン一つ一つにレーザーを照射するイオントラップ、液中の分子の核スピンを調べるNMR(医療用装置MRIと似た装置)[4]、そして現在の半導体技術の粋をつくして作成したジョセファン接合による超伝導単一電子箱[5]などだ。 ただし、これらの実験では数キュービット程度のもので、従来のコンピュータより高速な量子コンピュータには百万キュービット程度が必要だとされていることを考えると、まだまだコンピュータと呼べるようなものではないかもしれない。 それにイオントラップ、NMR、ジョセフソン接合などの現在の方法の延長では、おそらく百万キュービットを実現するのは不可能で、大きなブレイクスルーが必要とされている。 ref. [2]”Quantum Mechanical Models of Turing Machines That Dissipate No Energy” P.Benioff, Phys. Rev. Lett. 48, 1581-1585 (1982) [3]P.W.Shor, Proceedings of the 35th Annual Symposium on the Foundations of Computer Science , 124, (1994) [4]”Quantum computing in molecular magnets”, M.N. Leuenberger, D.Loss, Nature 410, 789-793 (2001) [5]”Bulk Spin-Resonance Quantum Computation”, N.A.Gershenfeld, I.L.Chuang, Science 275, 350 (1997) 量子力学と計算機科学量子コンピュータの動作原理を理解しようと思えば、どうしても量子力学と計算機科学の知識が必要になる。とくに量子コンピューティングの場合では、よく眺めてみると、この二つの知識はまったく別ものというわけではなく、うまく対応していることにも気づく。 ●量子力学の基礎 量子コンピュータの計算原理そのものを理解することが目的なら、量子力学について知っておかなければならないこと(前提)はそれほど多くない。ただし、その前提というのは、どれも日常的な感覚からかけ離れているので、はじめのうちは受け入れるのが難しい。 量子コンピュータの計算原理の理解で重要なのは、主に次の3つの内容だろう。とりあえずはじめに抽象的で一般的な説明をしているが、わかりにくいようなら読み飛ばして、後で紹介している具体例を見るとよいだろう。 1.波動関数ψであらわされる系に対して、ある物理量fの測定をすると、その固有値fnのうちの一つが得られる。観測される値fnに対応する固有関数をψnと表すと、波動関数ψはその適当な線形結合で表されなければならない。したがって、関数ψは次の形に表すことができる。 ψ=Σanψn 2.ある系を観測すると、重ね合わせの状態ではなく、その固有値の一つだけが観測される。つまり、観測することで、重ね合わせの状態はある状態へと収縮してしまう。このことを「波の収縮」などと呼んでいる。 また、どの固有値が観測されるかという確率は、それに対応する固有関数ψnの定係数anの絶対値の二乗に比例する。これは「ボルンの解釈」などと呼ばれている。 3.波動関数には観測できるすべての物理量の情報が含まれており、それは量子力学の基礎であるシュレディンガー方程式で計算することができる。一般にシュレディンガー方程式は時間によって変化して行くので、そういった状態も時間変化をしていく。なお、こういった変化をよくユニタリ変化と呼んでいる。
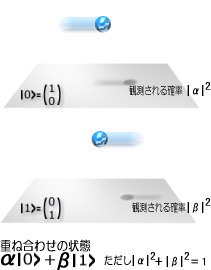
特に、上の二つはいかにも抽象的な感じがする。そこで直感に訴えるために、厳密ではなくても、具体的な一つの物理量を例に挙げてみよう。 例えば、図に示すように、粒子が右へ進んでいる状態(状態ベクトル|0>)と左へ進んでいる状態(|1>)があったとき、その重ね合わせ状態は”α|0>+β|1>”と表せる。量子力学によれば、この重ね合わせ状態を観測すると”|0>”が観測されることもあるし、”|1>”が観測されることもある。つまり、観測する前にあらかじめ粒子がどちらの方向に進んでいるか予測することはできないというわけだ。ただ、分かることは|0>と|1>が観測される確率がα、βそれぞれの絶対値の二乗になっているということだけだ。つまり、量子力学から確実に分かる唯一の情報は、確率だけということになる。 はみ出しコラム – 重ね合わせ状態のだまし絵
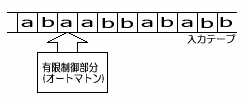
観測者によってある系の最終的な状態が決まってしまうというのは、日常感覚からすれば、簡単に受け入れられるようなものではないだろう。 ところで、この量子力学の重ね合わせの性質には、「ルビンの壷」や「老婆と婦人」といった「だまし絵」と似ているところがある。(科学的な根拠があるわけではなく、あくまで雰囲気程度の話だが…。)例えば、上に示しているルビンの壷は、中央に壷のある絵と2人が顔を向かい合わせている絵の二通りに見ることができる。確かにこのルビンの壷は、二つの絵の「重ね合わせ」と見なすことができるのだが、面白いことに、どちらか一方の絵に注意を払うと、途端にもう一方の絵を見ることができなくなってしまうのだ。つまり、壷の絵と同じに向かい合った顔の絵を意識することはできない。つまり絵の状態は観測者次第というわけだ。 他にこの性質を科学的に検証するものとして、半生半死の「シュレディンガーの猫」の話がある。もともとこの話は、シュレディンガーが量子力学のこの性質の矛盾を指摘するものとして持ち出したものだったが、今では一般に量子力学の正しさを説明するものとして紹介されている。ただ、今でもこの猫についての解釈にはいくぶんの余地があり議論は続いている。 ●チューリング機械 計算機科学でよく登場するものに、「チューリング機械(チューリングマシン、turing machine)」というものがある。チューリングマシンは、全体を制御する有限制御部分(有限オートマトン)と、入力記号列が書かれている入力テープとからできている。入力テープを挿入すると、オートマトンのヘッドはテープに沿って動きながら、羅列した数字のデータを読み取り、計算処理後には、結果を出力する。オートマトン部分には、計算処理を行うためのプログラムが書き込まれている。
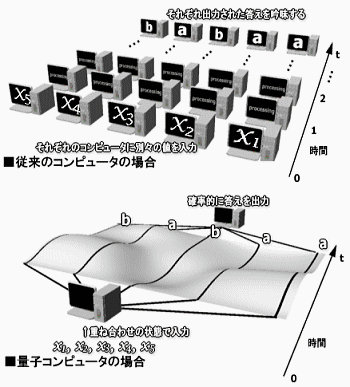
チューリング機械のモデル図 このチューリング機械と外見では似ていなくとも、現在のコンピュータの動作原理はすべてこれを基礎としている。 ●量子チューリング機械 チューリング機械をよく眺めてみると、上で紹介した量子力学と対応している箇所が多いことに気づく。例えば、入力テープに書き込まれている数字の羅列は、量子力学でとり得る状態に対応させればよい。また、制御部分であるオートマトンは、時間によって形を変えて行くシュレディンガー方程式、もしくはユニタリ変換と見なせばよい。したがってテープから入力された状態は、シュレディンガー方程式により変形されて、あらたにテープに出力され書きかえられる。 量子力学の性質を利用したチューリング機械には、従来のものと比較して大きな違いがある。それは重ね合わせの原理によって、入力テープに書かれている状態は重ね合わせになっているということだ。量子計算の基本となるこの情報量を量子ビット(キュービット、qubit)と呼ぶ。 そして、nキュービットのデータを扱うときは、一度入力テープを通すことで、従来の入力の2n回分の計算が行なわれていることになる。これが量子コンピュータが並列計算が可能だといわれる所以である。この違いを意識して、1985年にDavid Deutschは量子チューリング機械を導入した。[1]
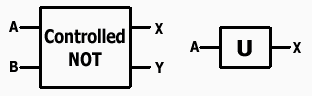
量子コンピュータと従来のコンピュータで並列計算を比較した場合(モデル図) ●量子回路 一般に電気回路は、多数の論理ゲートから構成されている。通常のコンピュータを実現するのに用いられている論理ゲートには、AND,NOT,OR,NORなどがある。それぞれの論理ゲートは非常に単純なものだが、例えばANDとNOT、またはORとNOTの二種類のゲートを用いれば、チューリング機械のどんな動作も模倣する回路を構成することができる。実際、現在のコンピュータは、このような回路から構成されている。 一方、量子回路も量子論理ゲートから構成されている。量子論理ゲートにもさまざまなタイプが存在し、世界中で量子回路のシミュレーションの研究が行なわれているが、特に制御NOTゲートとユニタリ変換ゲートが有名である。原理的には、この二種類の量子論理ゲートで量子チューリング機械のすべての動作を模倣することができるとされている。
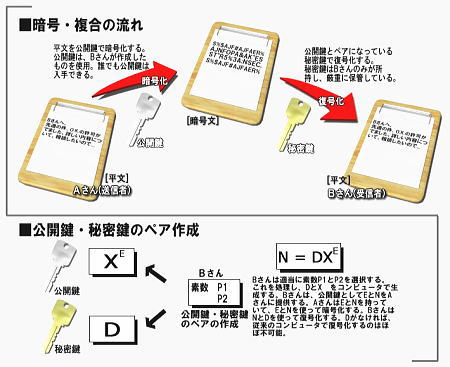
A.制御NOTゲート B.ユニタリ変換ゲート [1]D.Deutsch, Proc. R. Soc. Lond., Vol.A 400, pp.97-177(1985) Shorの因数分解アルゴリズム、他背景 かつて暗号というのは、軍事目的など、ごく限られた範囲でのみ利用されていた。ところが現在では、インターネット上の商取引や重要文書のやり取りなど (意識するかどうかは別として)、暗号は日常的に利用されるようになってきた。しかし、インターネットでは不特定多数の利用者が集まってくるために、従来のような暗号ではいろいろと都合が悪い。そこで登場したのが、「公開鍵暗号」という画期的なアイディアだった。 この公開鍵暗号の代表的なものに「RSA」暗号(RSAは開発者R.Rivest,A.Shamir,L.Adlemanの名前からとっている)というものがある。
このRSAのアルゴリズムは因数分解を基礎にしている。この原理を理解するために、次のクイズを考えてみよう。 次の値の素因数分解を行なえ。 ちゃんと因数分解はできただろうか?少なくとも紙と鉛筆だけで解くのは不可能だろう。では、こうしたら、どうだろうか? 次の計算を行なえ。 もう、何をいおうとしているのかお分かりだろう。つまり、 398477 x 299699 = 119423158423 について、左から右を計算することは簡単なのに、右から左を計算することは非常に難しいということだ(もちろん原理的にはとくことができるが、現実的な時間内にとくことが出来ない)。RSAは、因数分解のこの一方通行な性質を、上図に示すような暗号システムに対応させているのだ。 大きな値(例えば50桁)の因数分解は、現在のコンピュータにも苦手な問題といえる。公開鍵暗号というのは、コンピュータが現実的な時間内に大きな値の因数分解をとくことが出来ないということを安全性の根拠にしているのだ。 ところが、最も重要な暗号システムの一つであるRSAも、量子コンピュータの登場により、まったく無意味なものとなってしまう可能性があるのだ。量子力学的な「重ね合わせ」を利用することで、従来のコンピュータが宇宙の歴史ほどの時間をかけても解けなかったような因数分解を、量子コンピュータは数分、もしくは数秒で解いてしまうかもしれないのだ。この方法を具体的に示したのが、「Shorの因数分解アルゴリズム」である。このアルゴリズムは、量子コンピュータのキラーアプリとして、それまで学術的な範疇にとどまっていた量子コンピュータを社会全体の関心事にしてしまったのだ。 なぜShorのアルゴリズムか? さて、いざコンピュータに整数Nの因数分解をさせようとするとき、どのようなプログラムを考えればよいだろうか? まず誰でも思いつくのが、2,3,5….と2から(N-1)までの範囲にある素数を手当たり次第に探す方法だろうが、そのためにはあらかじめ(N- 1)までの素数表を入手していなければならない。しかし素数表といっても、RSAの因数分解は素数表を利用して簡単に解けるようなものではない。とにかく、この方法では量子コンピュータの利点をいかしきれない。 そこでShorが利用した因数分解の方法は、以前からよく知られていた次のようなものだった。これは剰余が一定の周期で繰り返すという周期関数を利用したものだ。(ここからやや数学的な予備知識が必要となるが、ページの下のほうで補足している。) 1.Nより小さいxを適当に選ぶ。 2.xとNの最大公約数fを計算する。f=gcd(x,N) [補足1] 3.xrをNで割ったとき、その余りが1となる最小の整数rを探す。[補足2] 4.(xr/2-1)とNの最大公約数、もしくは(xr/2+1)とNの最大公約数のいずれかが1以外の数字なら、それがNの素因数である。 5.ここまでで素因数が見つからなければ、1に戻って操作を繰り返す。 このような方法で因数が求められるのは、周期関数の特徴のためである([補足1]を参照)。また、最大公約数を求めるのは、ユークリッドの互助法を使えば、短い時間で簡単に解ける。 はじめてこのアルゴリズムを見た人には、なかなかピンとこないかもしれない。そこで、15の因数分解を例に考えてみよう。 1′. N=15より小さい数を適当に選ぶ。ここではx=11を選んだことにする。 このアルゴリズムで最も時間がかかるのは、ステップ3のrを探すことである。従来のコンピュータは、ステップ3でrを探すのに時間がかかりすぎてしまう。そのため従来のコンピュータでは、はやく素因数分解を行うという点で、このアルゴリズムを使うメリットは薄かった。ところが、Shorは「離散フーリエ変換」を使って、量子コンピュータがrを一瞬にして見つけられることを示したのだ。これがShorの因数分解アルゴリズムの核心部分である。 Shorのアルゴリズムの概要
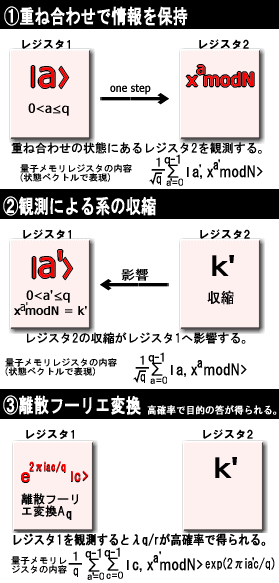
ここではShorの因数分解アルゴリズムの概要を述べよう。先ほどの項目で紹介したように、因数分解を効率よく行うためには、上手に周期rを探すことが重要となる。 そこで、二つの量子メモリレジスタ(レジスタは一時的に情報を蓄えておく場所)を用意する(右図)。 ①レジスタ1には、重ね合わせの状態で|a>(| >は状態ベクトル表示)を蓄えておく(a=0,1,2,…,q-1, n2<=q<2n2)。そしてこの重ね合わせの状態のまま、xamodNを計算する。このとき、従来のコンピュータならq回の処理を行なわなければならないが、量子コンピュータなら重ね合わせを利用して一括処理することが可能であることに注目しよう。この計算結果そのものも重ね合わせの状態でレジスタ2に蓄えられる。 ②つぎにレジスタ2を観測する。観測する前は重ね合わせだったレジスタ2の状態は、ある値k’に収縮する。レジスタ2の収縮はレジスタ1にも影響する。しかし、注意しなければいけないのは、レジスタ1の|a’>はxa’modN=k’を満たしている限りは、収縮せずに、重ね合わせの状態を保っているということである。なぜならxa’modNは周期関数なので、例えば xcmodN = xc+rmod = xc+2rmod = … =k’ とういように、a’がc,c+r,c+2r,…の重ね合わせの状態を保つことが出来るからだ。 ③そして、レジスタ1の|a’>を離散フーリエ変換する。この変換を行うことで、レジスタ1の状態は右図のようになる。この変換後にレジスタ1を観測すると、量子力学的な干渉により、 λ(q/r)、λ=整数 という整数が高い確率で観測される。こうしてrを決定することができる。以上の①~③までの操作は、重ね合わせや確率的動作など、量子コンピュータにしかできないものだとされている。しかし、いったんrが決まれば、あとは従来のコンピュータでも、「なぜShorのアルゴリズムか?」の方法にしたがってステップ4で最小公倍数を求め、Nの因数分解を行うことが出来る。 以上に紹介したことはShorのアルゴリズムの大まかな流れであって、その詳細や離散フーリエ変換の性質などについては、下で紹介している文献を参考にするとよいだろう。 その他の量子アルゴリズム ここでは詳しい内容に触れることはできないが、Shorのアルゴリズムの他にもGroverの検索アルゴリズムなどが有名である。N個のファイルのなかから特定のファイルを探し出す場合、古典的なコンピュータならおよそN/2程度のステップ数が必要なのに対し、GroverのアルゴリズムによるとN1/2ステップで高速に検索することができる。この差はファイル数Nが大きいときに明らかで、例えばN=1000のとき、古典的なコンピュータなら500ステップ数ほど必要なのに対し、量子コンピュータならたったの100ステップ程度ですむ。 また、量子スピン系や量子多体系の問題などについてのアルゴリズムも提案されている。 ref. ■数学的な予備知識 補足 [補足1]ユークリッドの互助法 ユークリッドの互助法とは、整数mとnの最大公約数を求める方法のことである(n>m)。nをmで割った余りをrとするとき、次のような操作を行なう。 1.r=0のとき、 2.r≠1のとき、 例. n=1029, m=42のとき、最大公約数は21である。
[補足2]周期関数 xとNが互いに素であるとき(x<N)、 例.x=11, N=15のとき
よって、この場合の周期r=2である。 実際に量子コンピュータを作るとにかく量子コンピュータの作成は難しい これまでに量子コンピュータの原理、いくつかの有用なアルゴリズムなどについて見てきたが、ここではどうやって量子コンピュータを実現するかを見てみよう。 まず言っておかなければいけないのは、確かに理論では量子コンピュータの動作が証明されているが、実際の物理系を使って量子コンピュータを実現することは途方もなく難しいということだ。はじめからRSAの暗号解読が出来るような量子コンピュータが作れると思ってはいけない。それどころか、現在の量子コンピュータというのは、私たちが頭のなかで解けるような簡単な問題がやっと、というレベルなのだ。 そこで、量子コンピュータの製作において、次のように何段階かの目標を決めるとしよう。
これは計算機科学としては非常に基礎的なことであるが、その実現は高いハードルの連続である。 なぜ、量子コンピュータを作るのは難しい? それでは、なぜ量子コンピュータを作るのがこれほど難しいのだろうか?その原因は二つある。 まず一つ目の原因として、量子コンピュータが周りの環境に対して余りにもデリケートすぎることが挙げられる。いわゆる「デコヒーレンス時間」の問題である。 量子コンピュータは重ね合わせの状態を利用することで超並列計算を行ない、これが量子コンピュータの強みとなっている。しかし、この重ね合わせの状態というのは、電子や光子をぶつけるなどして外部から観測することで、ある一つの状態へ解消されてしまう。この現象を「デコヒレーンス」という。そのため超並列計算を可能にするには、デコヒーレンスが起こらないように処理中に観測をしてはいけないことになる。つまり、計算が終わってからはじめて観測するというのが、量子コンピュータの正しい手順といえる。 ところが実際は、そう簡単にはいかない。なぜなら、量子コンピュータを外部環境から完全に分離することは難しく、処理を行なっている最中に外部から光子や電子がフラフラと入ってきて「観測」したことと同じになり、デコヒーレンスが起きてしまうからだ。これが環境に対してデリケートすぎるという理由だ。 結果として、計算処理時間よりもデコヒーレンス時間のほうが短ければ、正しい答えを得ることができない。量子コンピュータ実現の大きなハードルは、デコヒーレンス時間の短さにあるのだ。ただ、現在ではデコヒーレンスによって、答えに生じたエラーを訂正する方法が提案されており[1]、この状況は少しずつ改善されているようだ。 二つ目の原因は、「qubit集積化」の問題である。先ほどの量子誤り訂正の方法が提案されてから、ここ数年で量子コンピュータの研究はずいぶん進歩し、例えばIBMの研究チームのNMRを使った量子コンピュータはステップ3までをクリアしている。ただしステップ3まではあくまでアカデミックな色合いが強く、本当に実用的な量子コンピュータという点ではステップ4までクリアできなければならない。しかし現時点では、ステップ4、つまりqubit集積化をクリアできる明確な戦略を示すことのできている研究チームは一つもないのだ。なぜ集積化が難しいかは、次の具体例のなかで紹介しよう。 具体的な量子コンピュータ これまでの量子コンピュータの研究のなかで代表的なものについて、それぞれの原理、利点・欠点、また現時点で考えられている課題などを簡単に取り上げてみよう。 ・イオントラップ
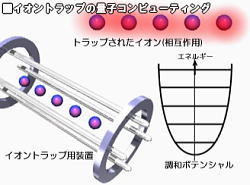
図に示すように、極低温、超高真空という条件下で、4つのロッドに高周波数の交流電圧を加え、その電磁場で目的のイオンを鎖状に並べている。両端のリングは、イオンが外へ逃げていかないためにとりつけてある。イオンどうしにはそれぞれクーロン力が働くので、ちょうど重りがバネによって数珠つなぎにされている状態と似ている。この見方はイメージをつかむのには便利だが、量子力学の支配する世界で、古典力学的な比喩を使うときは注意しなければいけない。なぜなら、量子力学ではエネルギーが離散的な値をとるように、バネの振動の仕方(振動モード)も限られたものだけをとるようになる。イオントラップの量子コンピュータは、この振動モードを量子ビットの|0 >,|1>に対応させている。これらのイオン一つ一つに狙いを定めて光子をぶつけることで、振動モードを重ね合わせの状態にしている。 この方法は量子コンピュータの動作原理の検証など、基礎研究で大きな意味を果たしている。ただし、ステップ4のqubit集積化については、装置が大掛かりになりすぎることもあって、現状のままでは実用的な量子コンピュータが実現することは難しい。現在、イオントラップの研究は、アメリカのNIST(National Institute of Standard Technology)が有名。(NISTはイオントラップを用いた新しい原子時計の研究などでも有名。) ・NMR
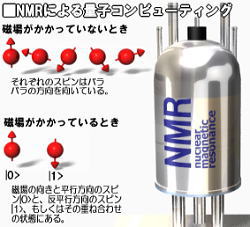
原子核は「スピン」という地球の自転のような運動を行なっている。ただしこの場合も、古典的な比喩はイメージをつかむのには便利だが、その使用には注意が必要である。磁場がかかっていないときは、スピンの軸方向は自由な方向を向いているが、静磁場がかけられている場合は、核スピンの軸方向は、磁場と平行と反平行の二つ状態しかとれない。軸方向が空間的に量子化されているというわけだ。 平行、反平行のそれぞれの状態を量子コンピュータの|0>,|1>に対応させている。反平行の状態は平行の状態よりもエネルギーが高い。このエネルギー差を考慮して、最適の周波数の電磁場を、強さを周期的に変えながらかけることで、核スピンの重ね合わせの状態を実現する。 NMRによる量子コンピュータは、イオントラップやその他のものと異なり、一つの原子に1qubitを実現しているのではなく、溶液中の多数の原子集団を1qubitとして扱っている。そのため、原子集団の中でいくつかの原子がデコヒーレンスを起こしても、集団の平均としては重ね合わせの状態を保っていられるため、デコヒーレンス時間が長いのが大きな利点である。 NMRの量子コンピューティングの研究はIBMが有名である。先ほども示したように7qubitを実現して、15についてShorの因数分解アルゴリズムを実行するなど、他の研究チームより頭一つ抜き出ている。ただし、NMRは原子数が増えると、NMRスペクトルが判別しにくくなり、単に分子を複雑なものにするだけではqubit集積化は難しい。 IBM’s Test-Tube Quantum Computer Makes History – IBMプレスリリース(2001) ・量子ドット リソグラフィーなどの半導体微細加工を用い、大きさが十数nm程度のドットを「量子ドット」と呼んでいる。量子ドット内の電子は、量子閉じ込め効果により離散的なエネルギー準位をとるようになる。特定のエネルギー準位aを|0>、エネルギー準位bを|1>とすることで、その差を考慮して最適なエネルギーの光子をぶつけることで、電子が二つのエネルギー準位の間を行き来する重ね合わせの状態を実現できる。 量子ドットは固体(ソリッドステート)であり、従来の半導体デバイスのように集積化の点では有利であるが、デコヒーレンス時間が短いことなどが問題となっている。量子ドットの量子コンピューティングは、国内では、NTT基礎研究所などが有名。 ・ジョセフソン接合 「ジョセフソン接合」によって外部電極と結合した微小な超伝導単一電子対箱を作り、ゲート電極を作用させることで重ね合わせの状態を作る。ジョセフソン接合とは、超伝導を利用して電流を抵抗なしで流すことができる回路で、ナノスケールの2つの超伝導体に薄い絶縁体が挟まれた構造をもっている。二つの超伝導体に電圧をかけていない場合はジョセフソン電流というトンネル電流が生じる。逆に電圧をかけると、高周波振動を起こす。 量子ドット同様に集積化の点では有利であるが、デコヒーレンス時間の問題がある。NECの中村研究チームが有名[2]。 世界で初めて固体電子デバイスによる量子コンピュータの回路開発に成功(プレスリリース1999) ref. リンク集ナノエレクトロニクスより スピントロニクス 外部リンク 国内 ERATO今井量子計算機プロジェクト 海外 IBM Almaden研究所 ニュース&解説 概論 量子コンピュータの基礎の基礎「量子重ね合わせ状態」に挑戦する – ZDNet(2003/5) 量子アルゴリズム Shorの因数分解アルゴリズム Papers Available Electronically – AT &T Grooverの検索アルゴリズム What’s Quantum Phone Book? – Bell Lab 量子コンピュータ実証装置 NMR IBM’s Test-Tube Quantum Computer Makes History – IBM(2001) イオントラップ Quantum Logic Experiments with Trapped Barium Ions – IBM ジョセフソン接合 量子コンピューター実現に向けた新しい電子集積回路を提唱 – 理研(2002/10) 量子ドット |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||